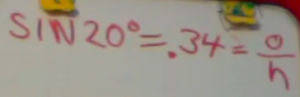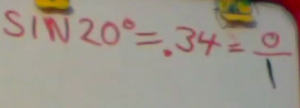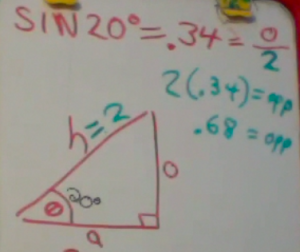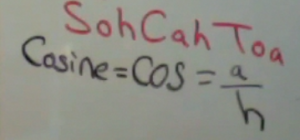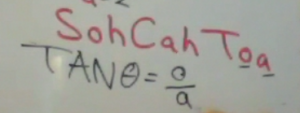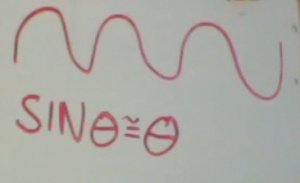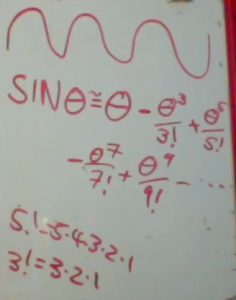So what do you do when you have triangles that are not 30-60-90, 45-45-90 or 3-4-5. And where did that 37-53-90 angle for the 3-4-5 triangle come from anyways?
You may have heard mention of the sine wave or sine function which looks like the above wave. The wavelike nature of the sine function will be treated later this year. For now, we will examine the relationship of the sine function to simple right angle triangles.
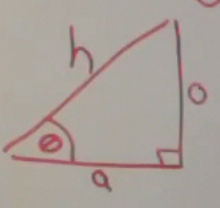
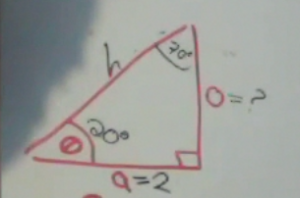
If we take a right triangle with an angle θ, we can label the sides of the triangle. The side of the triangle next to the angle θ we call the adjacent (a) side of the triangle. The side of the triangle opposite the angle θ we call the opposite (o) side of the triangle. And the long side of the triangle we call the hypotenuse (h).
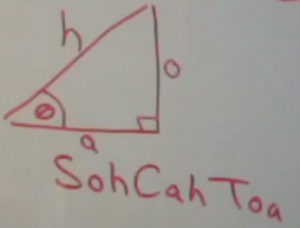
Using these labels, we have a mnemonic that can be used to remember the relationship between the length of the sides of a triangle and the angles in that triangle.
SohCahToa
S is for Sine(SINon your calculator)
C is for Cosine(COS on your calculator)
T is for Tangent (TAN on your calculator)
o is for opposite
a is for adjacent
h is for hypotenuse
So the Sine of the angle θ is equal to the length of the opposite side divided by the length of the hypotenuse
To actually calculate the sine of an angle by hand is tricky, and we will address this later. In the old days, one had to memorize a trigonometry table. Now, you can hit a button on your calculator. So when you enter Sin 20° on your calculator, it approximately gives you 0.34 (Note, your calculator has two angular units, radians and degrees. This is similar to inches and centimeters. They are just different units for measuring the same thing. You need to make sure your calculator is in DEGREE MODE. If you are using a TI-84, if you hit the MODE key, it will toggle you into the degree mode).


So if you enter the sine of 20 ° you get 0.34. The (absolute value of the) sine of an angle is always greater than zero and less than one. This is because it is the ratio of the length of the opposite side to the length of the hypotenuse. Since the hypotenuse it the longest side of the triangle, the sine has to be between 0 and 1.
Now let us examine a 20° triangle where the hypotenuse has a length of 1.
In that case, using simple algebra, we can find the length of the opposite side of the triangle.
Likewise, let us examine a similar 20° triangle, but this triangle has a hypotenuse of length 2. In this case, the opposite side will be twice as long or 0.68
If we want to examine the relationship between the adjacent side and the hypotenuse, then we use the cosine function. The cosine of an angle is the length of the adjacent side divided by the length of the hypotenuse.
In this case, let us still examine the triangle with a hypotenuse of 2. The cosine of 20° = 0.94 Solving by cross-multiplying, we get a length of 1.88 for the length of the adjacent side.
But what if we only have the adjacent side, and want to find the opposite side? Which trig function do we use?
We would use the Tangent function, which is the ratio of the length of the opposite side to the length of the adjacent side.
Let us use a triangle with an adjacent side of 2. In this case, we first take the tangent of 20°, which gives us 0.36. Solving by cross multiplying we get the length of the opposite side as 0.72
So what are these mysterious trig functions? How are they more than a button on our calculator? If you were to graph a sine (or cosine) function it would look like a wave.
A good approximation for small angles is that the sine of θ is approximately equal to θ itself.
But in truth, the sine function is more complicated. It is actually an infinite series. You could learn more about this using a Taylor Series expansion.
It is a giant polynomial function, with alternating positive and negative terms that get increasingly smaller. They are divided by factorial terms.
If this seems complicated….don’t worry about it now.
Vector Components
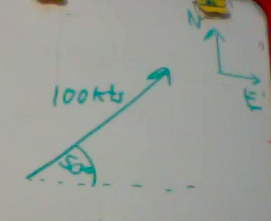
Suppose we have an airplane flying at 100 knots. The direction of the airplane is 50° north of due east.
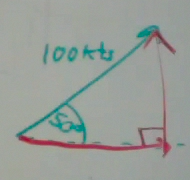
We could find the velocity in the northern direction and the velocity in the eastern direction by finding components using trigonometry. First we draw a right triangle.
Then we use trigonometry to find the sides of this triangle. These are called vector components. We use sine to find the northerly component.
And we use cosine to fine the easterly component of the velocity.