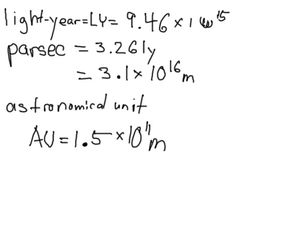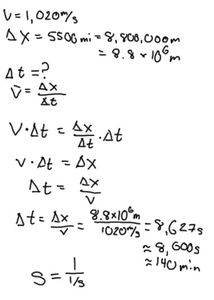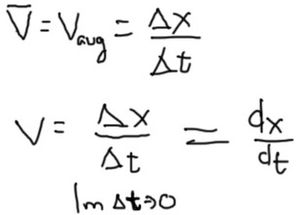The study of motion is often called kinematics. We will begin our study with one dimensional kinematics. We will later expand to 2 and 3 dimensional kinematics after we have studied vectors.
We can give the position of an object in relation to a reference point. There are a number of variables we can use for position, such as x, d, or s. The official metric unit for position is the meter (abbreviated m). The meter was first defined in terms of the circumference of the Earth on a meridian passing through Paris. It is now defined in terms of the speed of light. When working with other scales, it might be convenient to use other metric units such as the nanometer (nm), the centimeter (cm), and the kilometer (km).
Exponential Notation
We will often use exponential notation. Exponential notation is convenient for expressing very large and small numbers.
For instance, 12,300 would be expressed as 1.23 x 10,000 or 1.23 x 104
So 3.14 km = 3140 m = 3.14 x 103 m
For small numbers, 0.000345 = 3.45 x 10-4
A micrometer, 1 μm = 10-6 m The width of a human hair on average is 10 μm. This would be 10 x 10-6 m.
The wavelength of a helium-neon laser is 633 nm = 633 X 10-9 m = 6.33 x 10-7 m
Metric Units
The common metric units are given in powers or 3.
The kilometer is 1000 m.
Although the 100 centimeters = 1 meter it is not actually a common unit.
1 Millimeter = 1mm = 10-3 m
1 Micrometer = 1um = 10-6 m
1 Nanometer = 1nm = 10-9 m
1 Picometer = 1pm = 10-12 m
1 Femotometer = 1fm = 10-15 m also known as a Fermi
Except for kilometer, we often do not use the larger metric prefixes for distance. But they are used for frequencies and other units in physics.
1 Kilometer = 1 km = 1000 m = 103 m
Megameter = 1Mm = 106 m
Gigameter = 1Gm = 109 m
Terrameter = 1 Tm = 1012 m
Imperial Units
Common British Imperial units for measuring distance include the inch, the foot, the yard, and the mile. An easy way to remember the conversion from meters to miles can be remembered in terms of Track and Field. The loop in a track is ¼ mile long. It is also known as the 400 m race, so 1 mile is approximately = 1600 m. Engineers in America commonly use Imperial units. Very small measurements for the purposes of manufacturing are given in 1/1000ths of an inch.

When dealing with astronomical distances there are other units we might use such as the light-year, the parsec, or the Astronomical Unit. The light-year is the distance light will travel in one year. An object which is one parsec away has one arc-second of parallax from Earth. An astronomical unit is the average distance from the Earth to the Sun.
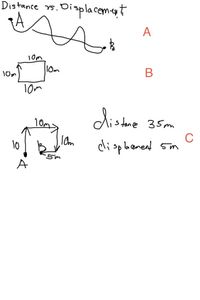
Distance vs Displacement
In physics we often study the change in position of an object. If we are only examining the change in position from the start of our observation to the end, we are talking about displacement. We ignore how we get from point A to point B. We are only concerned with how the crow flies. If we are concerned with our path, we are working with distance (see figure A).
For example, let us suppose I were to talk around the perimeter of a square classroom (see figure B). The classroom is 10 meters on a side. At the end of my trip I return to my original starting position. The distance traveled would be 40 m. The displacement would be zero meters because displacement only depends on the starting and ending positions.
The other important distinction between distance and displacement is that distances do not have a direction. If you were wearing a pedometer is would record distance. The odometer on a car records distance. Displacement has a direction and a magnitude. Magnitude is a fancy physics term for size or amount.
For instance, suppose I walked 10 m North, 10 m East, 10 South, and then 5 m West (see figure C). My distance traveled would be 35 m. There is a magnitude but no net direction. Since we can describe distance with just a magnitude (but no direction) we call it a scalar. But my displacement would be 5 m due East. As displacement has both a magnitude and a direction, we call it a vector.
Time
We measure time in seconds. We will use the variable t for time. The elapsed time for a certain action would be ΔT. The Greek letter delta, Δ, is used to represent a change in a quantity. If we are talking about a reoccurring event (such as the orbit of the Earth around the sun) we talk about the Period of time T, with a capitol T.
For longer periods of time we will often use the conventional minutes, hours, days, or years. For shorter periods of time will often use exponential notation or may use milliseconds, microseconds, picoseconds, or femtoseconds.
For instance, chemical reactions may often take place on the picosecond timescale. Just as when you dance un der a strobe like at a cool school dance you can see your movements in stop action. Scientists use pulsed lasers with picosecond and femtosecond pulses to examine dynamics at the molecular level.
der a strobe like at a cool school dance you can see your movements in stop action. Scientists use pulsed lasers with picosecond and femtosecond pulses to examine dynamics at the molecular level.
Speed and Velocity
Building on changes in position and changes in time, we can examine the rate at which these changes in position take place. How fast are we moving? You probably use the terms speed and velocity interchangeably in your everyday vernacular, but in physics they have distinct meanings. Speed is a scalar and has no direction. Speed can be defined as
speed = distance/elapsed time
Velocity is a vector. We could consider velocity to be speed in a given direction. To calculate the average velocity over a period of time, we use displacement and elapsed time.
Where v is velocity, x is position, t is time. The Greek letter delta, Δ, means a change in a quantity, such as the change in position or the change in time. The bar over the velocity v means the terms in averaged. For instance, Δx = xf – xo , or the change is position equals the difference of the final position and the original positions.
Our first set of problems will involve the above kinematic equation.
Problem Solving Method
When solving physics problems, it is useful to follow a simple problem solving strategy. Although at first, it may be easy to solve some problems in your head, by following this strategy you will develop good problem solving habits. Just as you must develop good habits by brushing your teeth every day, you should attempt to follow the following methodology for solving physics problems. The first step is Step 0 because it does not always apply.
Step 0: Draw a picture of the problem if appropriate.
Step 1: Write down the given information
Step 2: Write down the unknown quantity you are trying to find out
Step 3: Write down the physics equations or relationships that will connect your given information to the unknown variables.
Step 4: Perform algebraic calculations necessary to isolate the unknown variable.
Step 5: Plug in the given information to the new equation. Cancel appropriate units and do the arithmetic.
Example problems:
Example 1: A robot travels across a countertop a distance of 88.0 cm, in 30 seconds. What is the speed of the robot?
In this case, we do not need to do any algebra.
Significant figures: At this point we should not how many significant figures our answer has. Your final answer cannot have more information that your original data. We were presented with a distance and a time with only 3 significant figures, therefore our final answer cannot have more precision than this.
Now let us look at a problem which does require some algebra.
Example 2: The SR-71 Blackbird could fly at a speed of Mach 3, or 1,020 m/s. How much time would it take the SR-71 to take off from Los Angeles and fly to New York City via a path which is a distance of 5500 miles.

You should note that you need to convert miles to meters, remembering that 1 mile = 1600 m
First we need to algebraically isolate the variable t .First we multiply both sides by t, and t cancels on the right hand side of the equation.
Then dividing both sides by v gives us
Now, plugging in for distance and speed gives us
Note the units and the number of significant digits. Because one piece of our original data (distance) only had two significant digits, we have to round off our final answer to 2 significant digits. Also, look at the cancelation of units. The meters in the units cancel. Our units have the reciprocal of a reciprocal, thus the final units are in seconds, which you might have guessed since we are working with time. For ease of perspective we converted these units into minutes.
Average velocity vs instantaneous velocity
Another important distinction is finding an average value or the velocity versus the velocity at a given instant in time. To find an average velocity we only the measure the change in position and the total elapsed time.
However, finding the velocity at a given instant can be tricky. The elapsed time for an instant has no finite length. Similarly, a physical position in space has no finite size. To calculate this using equations we would have to reduce the elapsed time to a near infinitesimally small amount of time. Mathematically, this is the basic for calculus which was developed separately by both Newton and Leibniz. In standard calculus notation we would say the instantaneous velocity can be expressed as
In our next lesson we will learn how to determine the instantaneous velocity using graphical techniques.