Rotational Motion
So far this semester in our study of classical mechanics we have studied translational motion. We are now going to begin to explore rotational motion.
Every concept we have studied so far has a rotational analogue.
In the beginning of the year we discussed how an object could undergo a displacement x. We could also rotate an object through an angle θ.
Likewise, the velocity of an object or the rate of change of position
![]()
has its rotational analogue, the rotational velocity, the rate of change of angle
ω=Δθ/Δt
There is also an angular acceleration which is the rate of change of the angular velocity. We can examine torque, which is a rotational force. The moment of inertia (or rotational inertia) is the tendency for an object to stay at rest or stay in a state of rotational motion. Building on that, angular momentum is rotational inertia in a state of rotational motion. We also can have rotational kinetic energy!
Frequency and Period
If we assume an object is continuously rotating, then another way to look at rotational motion is to examine the period of rotation, T. Measurable in units of time (milliseconds, second, hours, years, eons…) the period is how much time is takes to make one complete rotation. We could also describe how frequently the object rotates. The frequency, f, of an object is actually the inverse of the period of rotation.
T=1/f
and
f =1/T
The metric unit for frequency is Hertz (Hz), where 1 Hertz = 1 cycle/second. You are probably familiar with the term Hertz from frequencies on the radio dial such as WBUR 90.9 MHz or WBZ 1030 kHz.
Example
Imagine a small boy tries to make himself dizzy by spinning around rapidly. If he spins at a frequency of 0.8 Hz, how much time does it take him to make 1 rotation?
f= 0.8 Hz
T = 1/f = 1/0.8 Hz = 1/0.8 cycles/second = 1.25 seconds
Another traditional unit for frequency is revolutions per minute or rpm. You might see this on an old fashioned record player which could rotate at 33 or 45 rpm.
Tangential Speed
For now consider two little LEGO men standing on a record player. As the record player turns, we can describe the motion of the little LEGO men in terms of their linear speed (meters/second) or their rotational speed. If we set the record player to 45 rpm, then both LEGO men have the same rotational speed. However, they have different linear or tangential speeds. We use the word tangential because if the LEGO man were to slip and fall, his own inertia cause him to fly off the record player on a line tangent to his circular motion!
We can calculate the linear speed for each man using the equation
v=2πr/T
where r is the radius of the circle and T is the period of rotation. Remember, speed is distance over time. In this case, the distance for one period of rotation happens to be the circumference of a circle.
If the men are located on our record player at positions 10 cm and 4 cm from the center axis:
Example
f = 45 rpm
r = 12 cm
First we calculate the period. Since 45 rpm = 0.75 revolutions/second
Thus the period of rotation is 1.33 seconds.
Thus the speed will be
v= 2πr/T = 2π (10 cm)/ 1.33 sec = 47 cm/s
For the little man who is standing at radius of 4 cm, he has a much smaller linear speed although the same rotational speed
v= 2πr/T = 2π (4 cm)/ 1.33 sec = 19 cm/s
Linear velocity vs angular velocity
There is a subtle difference between rotational speed and rotational velocity, which we will introduce at a later time.
We can define the relationship between linear velocity and angular velocity with the following equation
v = ω r
Notice, that ω, the angular velocity, was defined earlier as the change in angle per unit time.
ω=Δθ/Δt
Examining the above equation there is an interesting question as to the units for angular velocity. Up until now we have used terms such as revolutions per minute or rotations per second. But a revolution would be defined as one COMPLETE turning through 360°.
You have probably studied the units for angles in terms of degrees. But when we discuss angular velocity we usually are not talking about an integral number of rotations. Thus we could have to use units such as degrees/second. However, the degree is not the metric unit of rotation. The standard unit is actually the radian.
2π radian = 360°
If we look at a picture of a unit circle we can see the conversion between radians and degrees. They are really the same thing, just different units.
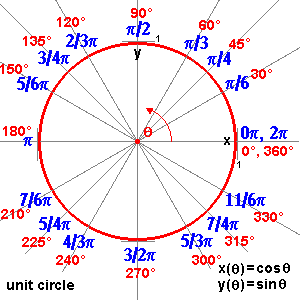
In one sense, the only difference between frequency and angular velocity is a matter of units. Angular velocity is measured in radians/second and frequency is measured in Hertz or rotations/second. Thus we could express an algebraic relationship between these two terms as
2πf = ω
Using this, we could actually find the angular velocity of our record player which spins at 45 rpm.
ω = 2πf = 2π (0.75 rev/second) = 4.7 radians/second
Example
Let us revisit the LEGO men on the record player. Using the relationship between linear velocity and angular velocity, we find,
v = ω r
v = 4.7 radians/second x 10 cm = 47 cm/s
and for the man closer to the center
v = 4.7 radians/second x 4 cm = 19 cm/s
It is important to note that the linear speed increases with both the angular speed and the radius
