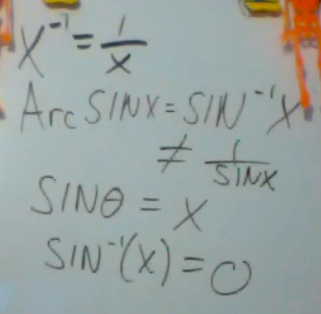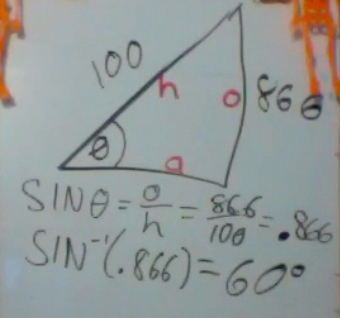When trying to find the angle in a right triangle, we can use the inverse trigonometric functions, or arc-trig functions.
Do not confuse this with the reciprocal functions.
An inverse sine function, (also called arcsine) runs the sine function in reverse.
If SIN θ = x, then ArcSIN x = θ
Here is an example where we are given two sides of a triangle. The hypotenuse is 100, and the opposite side is 86.6 We want to find an unknown angle θ.
Since SIN θ = o/h = 86.6/100 = 0.866 then we take the ArcSIN of 0.866 to get 60°
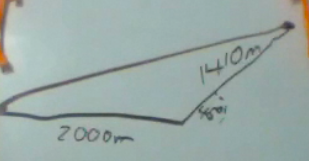
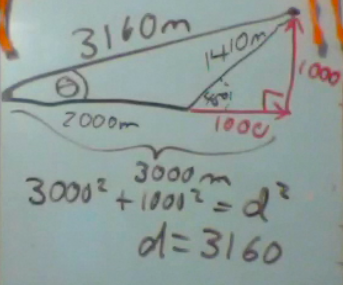
Here is a harder vector problem that you will see in the homework. Let us say you travel for 2000 meters east. Then you walk 1410 meters Northeast at 45°. You want to find the total displacement.
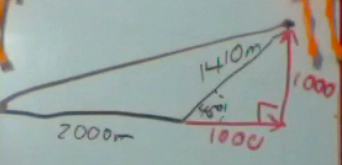
First you must break the 1410 into horizontal and vertical components. Since it is a 45° triangle, we don’t even need trigonometry. The components are each 1000 m.
Then we use the Pythagorean theorem to find the total displacement.
However, displacement has a magnitude and a direction. How do we find the angle θ? We use the ArcTAN function.
The side opposite θ is 1000, and the adjacent side is 3000. So we take the ArcTAN of (1/3) to get 18°