Many structures have a natural or resonant frequency at which they will vibrate when energy is transferred to them. A simple pendulum is an example of such a system. The natural frequency of the pendulum can easily be altered by changing its properties.
A simple pendulum can be modeled by a mass swinging back and forth on a massless string. If you account for the mass of the string (or of a rigid rod) then you must account for the distribution of mass described by the physical pendulum.
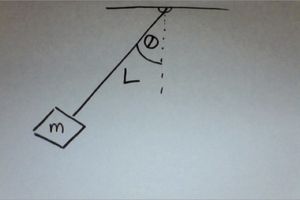
A pendulum swings back and forth through an angle θ. If we ignore friction, we can say the pendulum is oscillating back and forth. The length of the pendulum is L. The mass of the plumb bob is m.
You can watch an introduction to the pendulum here. Introduction to Pendulum
Legend has it that Galileo first noticed that the period of a pendulum is isochronous when observing swinging chandeliers in church. The term pendulum actually comes from pendulus,the Latin word for hanging . Galileo’s experiments show that the period of the pendulum varied with the square root of the length.
Later, in1673, Christian Huygens provided in his Horologium Oscillatorium a full analysis of the period of the simple pendulum. Now known as Huygen’s Law, he explained that the period, T of a pendulum depends on the square root of L, the length of the pendulum and g, the acceleration due to gravity.
Often we talk about the frequency which is actually the reciprocal of the period.
This equation can be derived for a simple pendulum can be using Newton’s Laws, rotational motion, and/or conservation of energy. This equation is often used in many standard physics problems.
There are two forces on the pendulum bob, tension and gravity. As a pendulum swings back and forth, its motion can be approximated with Simple Harmonic Motion.
You can use a computer simulation to model the behavior of a pendulum.