Wave Equation
As we have seen in class, the wavelength and frequency are inversely proportional to each other. Additionally, the wave speed is proportional to the wavelength. Thus we can express this relationship as
v = λf
where v is the wave speed, λ is the wavelength, and f is the frequency. Remember, the frequency is the reciprocal of the period of oscillation T.
f = 1/T
A concrete way to think about what this equation means is in terms of a wave train
Suppose our choo-choo train is traveling with a speed v. We know the definition of speed is
v= Δd /Δt
We can define each train car as one wavelength.
Δd = λ
In a given time Δt, the train travels an entire wavelength (one Period of time T).
Δt= T
Thus we can substitute into the equation for speed and arrive at
v = λ /T = λ f
wave speed = frequency x wavelength
Example:
What is the wavelength of Boston University Radio WBUR whose frequency is 90.9 MHz.? Radio waves travel at the speed of light so v = 3 x 108 m/s
v = 3 x 108 m/s
f = 90.9 MHz = 90.9 x 106 Hz
v = λf
λ = v / f = [3 x 108 m/s] /[ 90.9 x 106 Hz] = 3.3 meters
Note the units for wavelength are in meters! The Hertz cancel out with the per seconds.
Reflected Pulses
In class you observed what happens to pulses and waves when they reflect off of surfaces. You may have noticed that the PHET waves on a string simulation allowed you to chose a FIXED END, LOOSE END, or NO END.
With the fixed end, the reflected pulses are on the opposite side of the wave. You could think of this as akin to bouncing a ball. You could go into greater depth and explore boundary conditions. What this means is that the position of the reflected pulse just before it hits must be the same as the position just after. Likewise, the speed of the pulse must be matched (but opposite).
However, something strange happens with the free end. You might notice that it reflects on the same side. You can do this in the classroom by hanging a slinky/spring from the ceiling.
This Java Applet by BU Professor Andrew Duffy is also a great demonstration of this.
When running this simulation, you might notice that there is an option to create a boundary between two types of springs, heavy and light. In this case, two things happen. There is a reflected and a transmitted pulse.
Refraction and Wave Speed
In this video and the simulation, you may have noticed that the speed of the pulse changes at the boundary. If you go back and play with the PHET simulation, you will notice that the wave speed can be adjusted by changing the tension in the spring. The wave speed also depends on the inertia of the spring. You can read about the how inertia and tension affect the wavespeed at hyperphysics. Essentially
We will return to this idea when we talk about tuning a stringed instrument. Other factors will affect the wave speed for different types of waves. For water waves and the ripple tank, the wave speed actually depends on the depth of the water. The shallower the water, the slower the speed of the water.
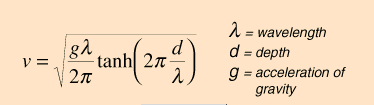A few numbers that are important to have on hand for typical physics problems. Radio waves, X-rays, microwaves, and light are all forms of electromagnetic radiation, and thus travel at v = 3 x 108 m/s
Sound waves travel in air at about 340 m/s. But this number can vary with air pressure, humidity, and temperature.
Sounds waves tend to travel much faster in a medium such as water (around 1500 m/s) or even higher in a solid such as steel (over 5000 m/s).
Energy in a Wave
What happens to the energy of a wave as it travels? As the wave travels, it loses a lot of its energy due to the friction of oscillating the medium through which it is traveling. In turn, this means that the amplitude decreases as the wave propagates. You may have noticed that you can adjust the “dampening” of the wave in the computer simulations. Additionally, at the boundaries, the question arises, how much energy gets transmitted versus how much is reflected?
