Energy in a Pendulum

In a simple pendulum with no friction, mechanical energy is conserved.  Total mechanical energy is a combination of kinetic energy and gravitational potential energy.   As the pendulum swings back and forth, there is a constant exchange between kinetic energy and gravitational potential energy.

Potential Energy

The potential energy of the pendulum can be modeled off of the basic equation

PE = mgh

where g is the acceleration due to gravity and h is the height.  We often use this equation to model objects in free fall.

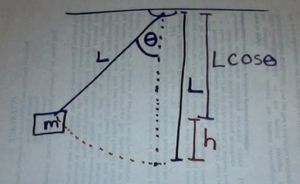
However, the pendulum is constrained by the rod or string and is not in free fall.  Thus we must express the height in terms of θ, the angle and L, the length of the pendulum.   Thus h = L(1 – COS θ)

When θ = 90° the pendulum is at its highest point.  The COS 90° = 0, and h = L(1-0) = L, and PE = mgL(1 – COS θ) = mgL

When the pendulum is at its lowest point, θ = 0° COS 0° = 1 and h = L (1-1) = 0, and PE = mgL(1 –1) = 0

At all points in-between the potential energy can be described using PE = mgL(1 – COS θ)

Kinetic Energy

Ignoring friction and other non-conservative forces, we find that in a simple pendulum, mechanical energy is conserved.   The kinetic energy would be KE=  ½mv²,where m is the mass of the pendulum, and v is the speed of the pendulum.

At its highest point (Point A) the pendulum is momentarily motionless.  All of the energy in the pendulum is gravitational potential energy and there is no kinetic energy.  At the lowest point (Point D) the pendulum has its greatest speed.  All of the energy in the pendulum is kinetic energy and there is no gravitational potential energy.  However, the total energy is constant as a function of time.  You can observe this in the following BU Physlet on energy in a pendulum.

If there is friction, we have a damped pendulum which exhibits damped harmonic motion. All of the mechanical energy eventually becomes other forms of energy such as heat or sound.

Mass and the Period

Your investigations should have found that mass does not affect the period of a pendulum.  One reason to explain this is using conservation of energy.

If we examine the equations for conservation of energy in a pendulum system we find that mass cancels out of the equations.

KE_i + PE_i= KE_f+PE_f

[½mv² + mgL(1-COSq) ]_i =  [½mv² + mgL(1-COSq) ]_f

There is a direct relationship between the angle θ and the velocity.  Because of this, the mass does not affect the behavior of the pendulum and does not alter the period of the pendulum.