This week has been perhaps a frustrating exploration of resistance and ohm’s law. Most of the links on this page will be to the hyperphysics website. The Ravenclaws made some impressive progress earlier this week. In fact they were quite on fire when they discovered the voltage drop across a wire in their experiment and started measuring the resistance of the wires in their experiment. As theory says, the longer wires have more resistance. The thicker wires have less resistance. Not all the wires followed these general observations as what was inside the insulation couldn’t be seen. Some wires might be aluminum vs copper.
An equation for resistance was mentioned last week for the resistance of a wire which is
where R is resistance, rho is resistivity, L is length, and A is cross sectional area. If you play with the computer model of a circuit, you will find you can actually simulate the resistivity of the wire, and measure the voltage drops over the wires. Click here for a table of resistivity values for different materials.
| Copper | 1.68 | x10^-8 | .0068 | 5.95 |
| Aluminum | 2.65 | x10^-8 | .00429 | 3.77 |
| Tungsten | 5.6 | x10^-8 | .0045 | 1.79 |
Now that we look a bit closer at that table, we don’t usually use tungsten for wiring….except in light-bulbs. But also, resistivity increases with temperature due to the motion of the atoms. Our power resistors, which do not get very hot were made from Carbon. The resistance of carbon doesn’t increase significantly with temperature compared to tungsten. However, the light bulbs had filaments made from tungsten. We measured the resistance of their filaments cold. But what happens when they are hot enough to glow? A possible error? Is the resistance of a hot light bulb different than a cold light bulb???? What did your textbook say?
Some of you may have gotten to combining your resistors in series and parallel. Where do those equations come from? Something to explore next week.
If you continue to play with the PHET simulations there are some other interesting things you might note. You can change the voltage of the batteries in the simulation. That is to be expected. But they have a feature called “internal resistance?” What is that? The Gryffindors suggested that the ends of the battery might have some resistance, thus making a difference between the 1.2V and 1.5 V batteries. Actually, all the magic is inside. This difference is actually due to the choice of chemicals, but more on that later.
The batteries have an internal resistance due to the rate of the chemical reaction. The real difference between a D cell and a AAA battery besides the amount of chemical potential energy stored is the amount of this internal resistance. And by placing batteries in parallel, we reduce the overall resistance due to these batteries. You can easily measure this internal resistance by measuring the voltage drop in the battery when there is no load versus when there is current running through the battery. So that 1.5 V battery might only put out 0.8 V when it is working really hard! Some of that chemical potential energy is becoming electric potential energy, but a lot of it might become heat! Feel the battery. Is it warm?
Some examples of the internal resistance for an old-style carbon-zinc battery:
AA battery 0.29 Ω
AAA battery 0.44 Ω
C battery .47 Ω
D battery 0.27 Ω
This returns us to what is actually happen in the battery and where those numbers such as 1.5 V comes from? There are two metals in the battery, the anode and the cathode. They both interact through the electrolyte. Each electrode has a half-potential and combines to create that 1.5V. So the reaction of Carbon with the electrolyte might generate +0.74 volts, and Zinc with the electrolyte might generate -0.76 volts, thus the total difference is 1.5 V. So the voltage depends on the chemical reaction, and not whether it is rechargeable. As an aside, wet-cell batteries, such as lead acid batteries often have a very low internal resistance, and can thus be very dangerous.
In chemistry you will study the electroseries for metals and what these half-potentials are. Here are a couple of examples.
| Nickel | Ni2+ + 2 e- | = | Ni | -0.257 | ||
| Cadmium | Cd2+ + 2 e– | = | Cd | -0.403 |
Keep in mind, it is not pure Nickel and Cadmium used in the electrodes. The actual reaction is
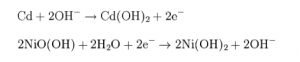 As a few closing thoughts. How does a meter work? The Hyperphysics site has a nice summary of meters. Volt Meters are always in parallel and measure the potential difference between two spots in your circuit. An ammeter is a flow meter and measures how much current is flowing through a single point in the circuit, thus it is always placed in series with the circuit. Placing an ammeter in parallel or directly to the battery can short it out. An ohmmeter measures resistance by sending a small current through your resistor or device. Thus it is measuring a current which it creates. So you cannot measure the internal resistance of a battery with an ohm meter, nor can you measure resistance when there is electricity flowing through a circuit from a power source. Internal resistance can be calculated by examining the voltage drop across a battery.
As a few closing thoughts. How does a meter work? The Hyperphysics site has a nice summary of meters. Volt Meters are always in parallel and measure the potential difference between two spots in your circuit. An ammeter is a flow meter and measures how much current is flowing through a single point in the circuit, thus it is always placed in series with the circuit. Placing an ammeter in parallel or directly to the battery can short it out. An ohmmeter measures resistance by sending a small current through your resistor or device. Thus it is measuring a current which it creates. So you cannot measure the internal resistance of a battery with an ohm meter, nor can you measure resistance when there is electricity flowing through a circuit from a power source. Internal resistance can be calculated by examining the voltage drop across a battery.
