Friction is generally a very complex topic when one considers the causes of friction on a microscopic level. What I will present here are several macroscopic generalization that can be applied in most instances.
Generally, the magnitude of the force of friction depends on the roughness of the material. The rougher or bumpier the material, the more friction there will be.
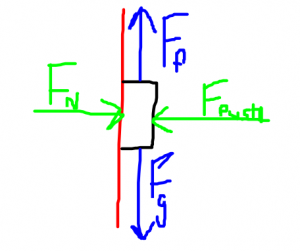
The magnitude of the force of friction also depends on the Normal Force. We usually think of the normal force as opposite to weight. If that were the case, then we could draw a free body diagram as this.
 So we have the force of gravity downwards, the normal force upwards, and applied “push” to the right and friction to the left. Note, that the force of friction is parallel to the two surfaces. As the strength of the normal force increases (which is the force between the “sliding” surfaces) the strength or magnitude of the friction also increases.
So we have the force of gravity downwards, the normal force upwards, and applied “push” to the right and friction to the left. Note, that the force of friction is parallel to the two surfaces. As the strength of the normal force increases (which is the force between the “sliding” surfaces) the strength or magnitude of the friction also increases.
We can consistently say that friction is parallel to the surfaces, and the normal force is perpendicular. In the above case, friction is horizontal.
However, we could just as easily have friction in a vertical or at an angle. Consider a person squeezing a bar of soap. Or a child sliding down a pole at the playground. In both of these cases, the normal force is NOT due to gravity, but due to the squeezing of the objects by someone’s hands. The normal force is perpendicular to the pole, and the friction is parallel to the surface of the pole.
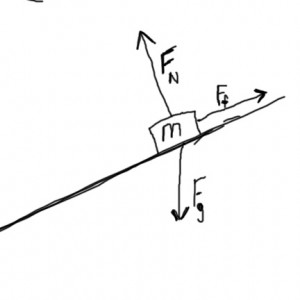
 Likewise, on an inclined plane, the normal force is still perpendicular to the surface, and friction is parallel. In this case, the Normal force is only of component of the weight.
Likewise, on an inclined plane, the normal force is still perpendicular to the surface, and friction is parallel. In this case, the Normal force is only of component of the weight.
When we have an object which is sliding over a surface, we call the resistive force either sliding friction or kinetic friction. The equation which describes the magnitude of this friction force is
Ff = μkFN
where FN is the magnitude of the normal force, and μ is the coefficient of friction. μ describes the bumpiness or roughness of the surface. μk will generally be a number between 0 and 1, and it has no dimensions. This makes sense if you examine that both sides of this equation have a Force expressed in Newtons. The k next to the coefficient is for kinetic.
With sliding friction you can generally think of the microscopic “bumps” in a material causing resistance (which is glossing over the truth regarding electrostatic forces). However, another form of commonly discussed friction is static friction. When you try to push an object it will resist you not only because of its own inertia, but because of the static friction between the object and the surface on which it is resting. In this case, you could think of the microscopic bumps as locking together like Velcro.
It is important to note, that static friction is only created in response to an applied force, similar to the way the Normal force is only created in response to an applied force. Because of this, when dealing with static friction, our equation actually has an inequality.
Ff ≤ μsFN
If an applied force is greater than μFN, then the force of static friction is overcome and the objects starts to slide. The s is for static in μs
Additionally, in most cases the coefficient of sliding friction will be less than the coefficient for static friction.
μk < μs
One important consideration about static friction is how the wheel works. When a wheel rolls on the ground, it is not sliding. So a rolling tire actually uses static friction to keep going. When your car skids or the wheels are locked, then your tires are sliding across the ground which is very dangerous. Again, we owe Ug the caveman credit for this great realization.
One interesting misconception is that the amount of friction depends on speed. Once an object is sliding, the amount of friction tends to be constant. Of course, friction generates heat, and this could change the properties of a substance.
Another type of friction involves fluid dynamics. In your everyday like, you might think of this as air resistance, but it is not limited to air. Fluids includes both liquids and gases. The amount of fluid resistance does depend on the speed of the objects, the shape of the object, and the viscosity of the fluid.
Example:
Suppose an 8.2 kilogram dictionary is slid across a counter. If the coefficient of sliding friction between the book and the counter if 0.2, then what is the force of friction on the book?
m = 8.20 kg
μk = 0.200
Ff = ???
Ff = μkFN
Be cautious here that you do not plug in 8.2 kg for the Normal Force. Remember, this is a mass. From this mass you can calculate the weight, and in turn the normal force.
FN = mg = 8.2 kg x 9.8 m/s2 = 80.4 N
Then from here we can plug into
Ff = μkFN = 0.200 · 804 N = 16.1 N