We have all heard of Newton’s Three Laws of Motion, but if asked to recite them or interpret their meaning, most of us would get stuck. Newton’s Second Law often appears on T-shirts and billboards as
F = ma
Where F is force, m is mass, and a is acceleration.
There is a lot to be lost in this common simplification of Newton’s Second Axiom. If we examine what Newton actually wrote in his Principia, after several pages of definitions, Newton finally writes
Lex II: Mutationem motus proportionalem esse vi motrici impressae,
et fieri secundum lineam rectam qua vis illa imprimitur.
In translation (by Andrew Motte as Newton wrote in Latin) this becomes:
LAW II.
The alteration of motion is ever proportional to the motive force impressed;
and is made in the direction of the right line in which that force is impressed.
Newton then goes on to clarify:
If any force generates a motion, a double force will generate double the
motion, a triple force triple the motion, whether that force be impressed
altogether and at once, or gradually and successively. And this motion
(being always directed the same way with the generating force), if the body
moved before, is added to or subducted from the former motion, according
as they directly conspire with or are directly contrary to each other ; or
obliquely joined, when they are oblique, so as to produce a new motion
compounded from the determination of both.
Many of the terms here are actually references to momentum and the change in momentum of an object which we will explore in a couple of weeks. Avoiding this term for now, we can think of the alteration of motion as the acceleration. And the motive force as the sum of the forces on an object.
If I were to represent Newton’s Second law with an equation I would prefer to write it as
a = Fnet/m
where Fnet is the net force or the sum of the forces on the object which is being accelerated. So what this equation tells us is that several forces acting on an object of mass m, will result in an acceleration.
Acceleration a, and Force F are written with bold lettering because they are vectors, and have a direction. What this also tells us the the direction of the acceleration is the same as the direction of the Net Force. As Newton writes “in the direction of the right line in which that force is impressed.” His explanation and reference to oblique angles refers to vectors and when the forces are not co-linear.
If you remember, Newton’s first law built heavily on the work of Galileo. His second law should also give credit to Descartes and Wallis.
A reminder on the relationship between the units. In the metric system we are using the Newton (abbreviated as N) as the unit of force. Thus we can define
1 Newton = 1 kg∙ m/s2
Example 1:
Suppose that a 120 kg NASA astronaut on a spacewalk uses her rocket booster pack to accelerate back to the International Space Station. If the thrust delivered by the rocket pack is 24 N, what is the acceleration of the astronaut?
m = 120 kg
F = 24 N
a = ???
Fnet = ma
We isolate the acceleration to arrive at
a =Fnet/m
Plugging in for mass and force we get
a = 24 N/120 kg = 0.20 m/s2
Example 2:
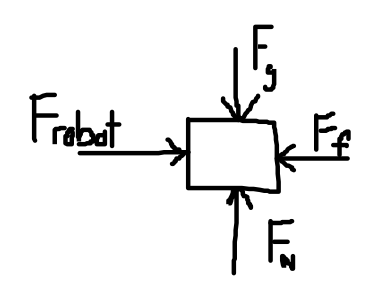
A book is pushed across the counter by a melancholy depressed robot. The robot pushes the book with a force 10.0 N. The force of friction is 4.00 N. What is the mass of the book if its resulting acceleration across the counter is4 m/s2?
In this case, it would help to draw a free body diagram as we have more than one force.
Frobot= + 10.0 N
Ffriction= – 4.00 N
Fnet = + 6.00 N
a = 4.0 m/s2
m = ???
Starting with Newton’s Second Law
Fnet = ma
We isolate m to arrive at
m = Fnet /a
Plugging in, we arrive at
m = (10 N – 4 N)/4.0 m/s2 = 6.00 N / 4.0 m/s2= 1.5 kg
It is worth noting how the units cancel out and the number of significant digits.
Example 3:
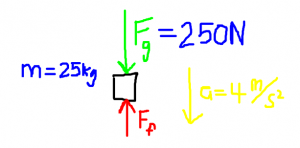
Alejandro Garber, who has a mass of 25 kg, slides down a pole at the playground. If Alejandro’s acceleration towards the ground is 4 m/s2, what is the force of friction between his hands and the pole slowing him down?
m = 25 kg
a = + 4.0 m/s2
Ffriction= ??
Looking at the free body diagram, we see the force of gravity is downwards and friction is upwards. If we define upwards as the negative direction and downwards as positive, then we can define the weight:
Fgravity= mg = 25 kg x 9.8 m/s2= 250 N
Since we know both the acceleration and the mass, we can find the Net Force.
Fnet = ma = 25 kg x 4.0 m/s2=100 N
Then, using our free body diagram, we can find the force of friction
Fnet = Fgravity – Ffriction
If we isolate Friction,
Ffriction = Fgravity – Fnet = 250 N – 100 N = 150 N