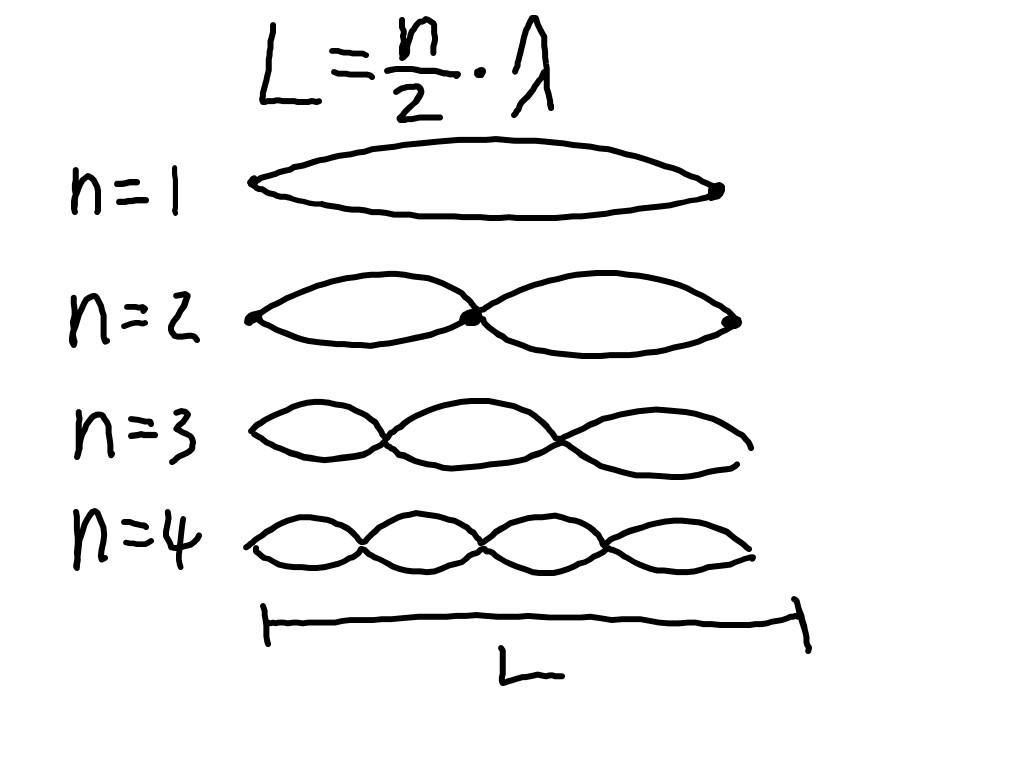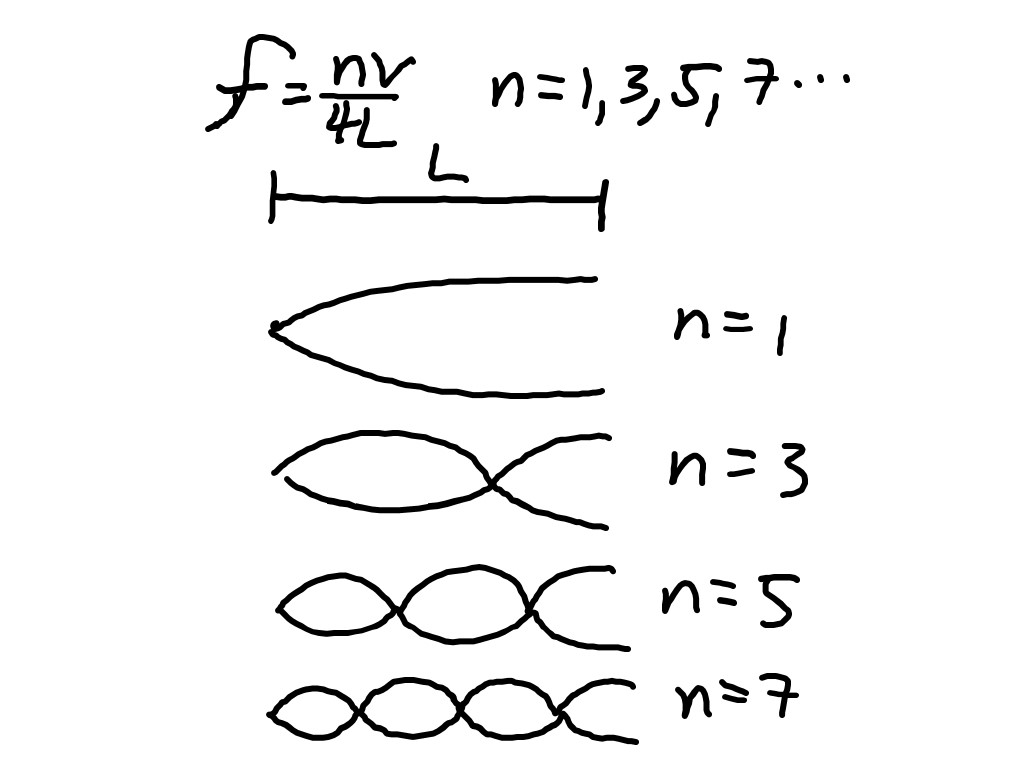In class this week we explored the causes of standing waves and what happens when they are produced in strings and pipes.
The important idea is that when a traveling wave hits a barrier there will be a reflection. If those reflections are timed exactly, then they will result in constructive and destructive interference in stationary locations. The locations where destructive interference occurs are called nodal points. At these nodal points, there is no movement of the string. The locations where constructive interference occurs are called anti-nodal points. At these points, the string would oscillate between Supercrests and supertroughs.
We also found for that a given string of a length L, with fixed end points, there can exist only half-integer number of wavelengths for standing waves on the string. λ is wavelength and n is an integer which happens to be equal to the number of anti-nodes.
We can further, using the wave equation, express this as the possible frequencies that a string will resonate at.
f = nv/2L
where f is the frequencies, and v is the speed of sound in the string. So actually presents us with an equation for the harmonic frequencies that the string will vibrate at. As the week progresses we will connect this to actual musical notes. This of course, related to the different kinds of sounds that we can here on string instruments. The pitch or frequency that we hear depends on the length of the string and on the speed of sound in the string. And the speed of sound depends on the bulk density and the tension in the string.
We looked at a case for a solid rod vibrating with loose ends. This sketch has the 1st, 2nd, 3rd and 4th harmonics.
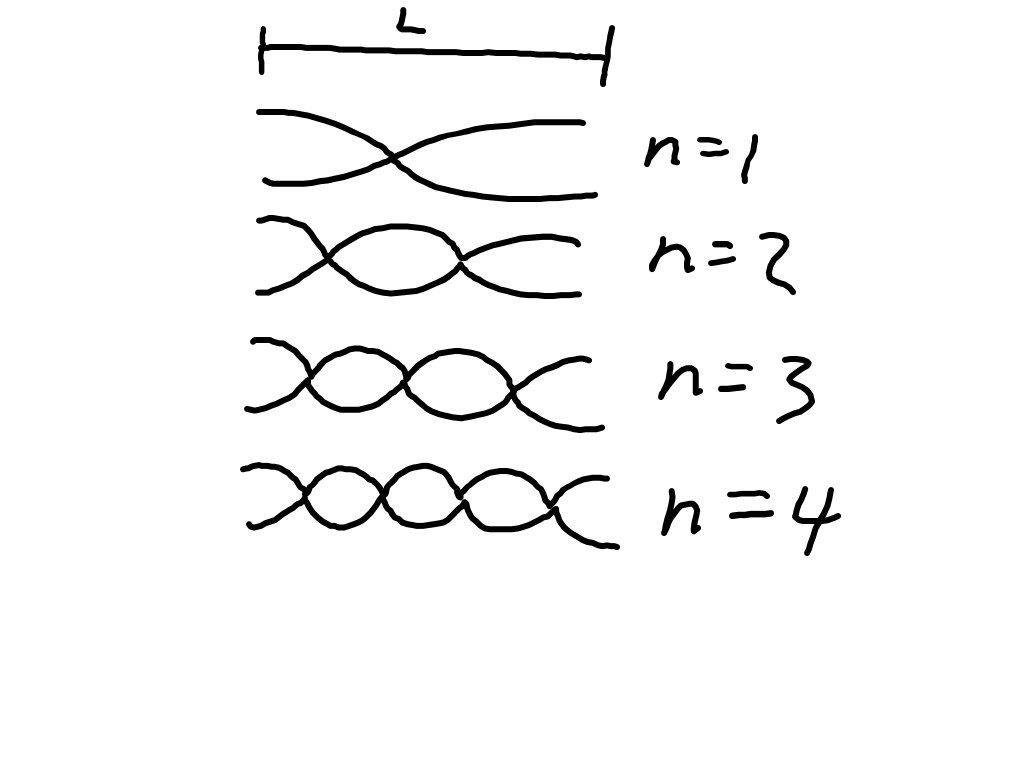 The harmonics for an open wind pipe would be identical to this as would be the equation. Even though there is a 1/4 wavelength at the ends, two quarters add up to a half. However, in a pipe, it is air that is vibrating so in the equation
The harmonics for an open wind pipe would be identical to this as would be the equation. Even though there is a 1/4 wavelength at the ends, two quarters add up to a half. However, in a pipe, it is air that is vibrating so in the equation
f = nv/2L
v is the speed of sound in air (about 340 m/s) and not the speed in the material.
Whereas for a closed pipe (such as s Coke Bottle), with one end open and the other end closed, there will be an odd integer number of 1/4 wavelengths.
Also, when thinking about a Coke bottle making noise, remember the Length L, is not the length of the bottle, but how much air is in the bottle. So if you fill it with water, you decrease the amount of air.