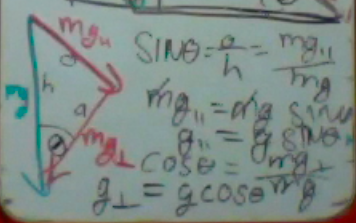We previously examined the kinematics of the inclined plane as Galileo might have in his experiments. We had not investigated the forces on an object on an inclined plane as Newton might. From a mathematical standpoint, this is the hardest set of problems we will study this year. Once you can get over this peak, the study of physics is all down hill from here.
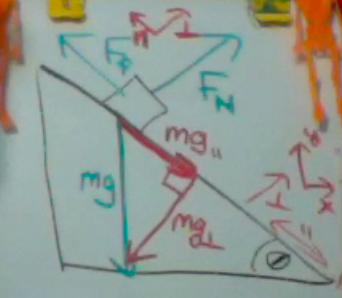
If we draw a free body diagram of a block on an inclined plane (that is an angle θ above the horizon), there are three forces: Friction, the Normal Force, and Weight. Weight, or the force of gravity is always straight downwards. The Normal Force is always perpendicular to the surface of the plane. Friction is always parallel to the surface. Depending on other forces or the direction of motion, friction could be in either direction parallel to the plane. If the object was sliding upwards, then friction would be in the opposite direction from what it is drawn in this diagram.
 In our previous vector problems, we would break diagonal vectors into horizontal and vertical components (x and y coordinates). We could do that here. However, since we would have to break up multiple vectors into components, and our direction of motion is parallel to the plane, it is easier to use a coordinate plane which is perpendicular and parallel to the surface. In this case, we actually break gravity or weight (symbolize by mg in this sketch) into components. These two components are smaller than the weight itself. Weight parallel is along the plane, and weight perpendicular is at a right angle to the plane.
In our previous vector problems, we would break diagonal vectors into horizontal and vertical components (x and y coordinates). We could do that here. However, since we would have to break up multiple vectors into components, and our direction of motion is parallel to the plane, it is easier to use a coordinate plane which is perpendicular and parallel to the surface. In this case, we actually break gravity or weight (symbolize by mg in this sketch) into components. These two components are smaller than the weight itself. Weight parallel is along the plane, and weight perpendicular is at a right angle to the plane.
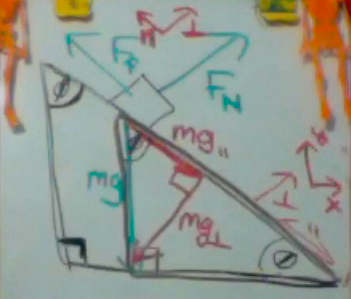
 Now we can fill in some angles. Our plane is an angle θ above the horizon. The complementary angle in the upper corner is φ. And there is of course a right angle. The angle between weight and the plane is also φ. Notice where we have similar triangles. The components of weight also form a similar triangle. But in this case, θ is in an unexpected location.
Now we can fill in some angles. Our plane is an angle θ above the horizon. The complementary angle in the upper corner is φ. And there is of course a right angle. The angle between weight and the plane is also φ. Notice where we have similar triangles. The components of weight also form a similar triangle. But in this case, θ is in an unexpected location.
 Here you see θ in the lower corner of our weight vector diagram. Now if we label the opposite, adjacent, and hypotenuse sides of the triangle, we can find the relationship between the weight components and weight itself. Since SINθ = o/h we can come up with an expression for weight parallel. Then notice that mass cancels out of this relationship! Thus g (9.8 m/s/s) itself can be broken into two components.
Here you see θ in the lower corner of our weight vector diagram. Now if we label the opposite, adjacent, and hypotenuse sides of the triangle, we can find the relationship between the weight components and weight itself. Since SINθ = o/h we can come up with an expression for weight parallel. Then notice that mass cancels out of this relationship! Thus g (9.8 m/s/s) itself can be broken into two components.
g parallel = g SINθ
g perpendicular = g COSθ
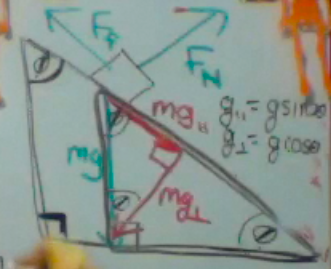 Looking at the above diagram, let us examine the dynamics in the perpendicular direction. Assume there is no acceleration perpendicular to the surface (otherwise the object would collapse the surface or fly up into the air). If there is no perpendicular acceleration, there is no net force in the perpendicular direction. There are only two perpendicular forces: The Normal Force and weight perpendicular. Thus for ALL inclined plane problems, we find
Looking at the above diagram, let us examine the dynamics in the perpendicular direction. Assume there is no acceleration perpendicular to the surface (otherwise the object would collapse the surface or fly up into the air). If there is no perpendicular acceleration, there is no net force in the perpendicular direction. There are only two perpendicular forces: The Normal Force and weight perpendicular. Thus for ALL inclined plane problems, we find
normal force = mgCOSθ
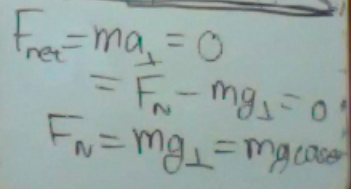 What happens in the parallel direction will vary depending on the problem.
What happens in the parallel direction will vary depending on the problem.
We will examine the case of objects accelerating on an incline plane in a few weeks. For now, let us consider the objects which is at rest on an inclined plane because of friction. In this case, the acceleration is zero. So the friction will be equal to the weight parallel. Remember, static friction is only as strong as the force impressed. A question to leave you with.