Gary Garber's Blog

On a related note, I found out today that the Tufts Department of Mathematics is starting a Math Circle. I will have to check it out!

But in Melrose, we finished today’s session of Math Circle playing the Keypad Game, which I first read about on page 1 in Gilman’s Book.  As the earlier games we played were not numerical, I wanted to get into a game with some arithmetic.

The full details of the Keypad Game can be read about in a 2007 edition of the College Mathematics Journal.   They have an article called the Number-Pad Game by Alex Fink and Richard Guy.    This is a fun game which can be played on a normal telephone key pad.

You can include the zero button, but for the game we played in class, we did not use the zero.   The rules are simple.  Firstus pushes any button.  Secondus must push a button in the same row or column.  Then firstus pushes another button in the same row or column as secondus (and may push the original button).  This goes back and forth until one player gets MORE than 30.  That player loses.

You can choose any # to be higher than, but we started out with the number 30 for a trial.  After the students played each other, I challenged them to beat me, which none of them could, but I cheated.  I knew that if I started playing with the # 9, and followed a certain pattern, it was impossible for them to beat me.

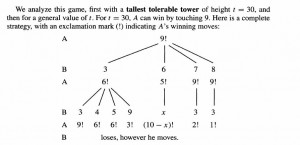
There is an interesting choices for the #30 as follows.

How to win for the number 30 starting with the number 9

As Fink notes, this game can be played for any number, or as he calls it, the Tallest Tower.  If you look in the table, you see that for the # 30, both 3 and 9 are winning first moves, but 9 will get you there quicker.

How to win for any number

Have a good February Vacation!

Last week I talked about the Reduced Gravity Pendulum at the Lowell Regional Physics Alliance. The LRPA is a great group of Physics Teachers from the greater Lowell area who gather once a month.  There is always a great keynote speaker, some cool demonstrations, and a few prizes.  The talks are organized by the legendary Art Mittler.

You can find a lot of the links from my talk in a previous blog posting from October when I gave this talk at Boston University Academy.   There are a few new links that I wanted to mention.  First, as I write this there is a new group of teachers currently flying on Reduced Gravity Flights in Houston.  You can see photos here.   You can also track their flight online.

Floating in zero g

Some teachers might be interested in their own proposals for a RGL, so I wanted to post a copy of my BUA application.  I hope that will help you in the writing of your own application.  I am also posting a copy of the Test Equipment Data Package (Boston_27Jun11_groupA_26June2011.)  This is the lengthy document you must write after you have been accepted (under the tutiledge of a NASA mentor) explaining how your experiment works.

I will try and upload the actual data in a couple of days.

For the next few weeks we will be exploring Game Theory.   What is Game Theory?  I have been reading a book by Rick Gilman, Models of Conflict and Cooperation. You can read the first several pages on Google Books.   According to Gilman, Game Theory is the study of the mathematics of decision making.  And since in Games, we need to make decisions every turn, it leads to great mathematical models, which can be applied to all realms of our daily lives which involve the decision making process.  One of the great minds of Game Theory was John Forbes Nash, who actually received the Nobel Prize in Economics in 1994 for his work in Game Theory.   For the parents, I strongly recommend the movie, A Beautiful Mind, which will give you some background into Nash's life.  The movie is PG-13, so I don't think I would show it to 3rd graders, but it will give you a Hollywood version of what we are doing in Math Circle over the next few weeks.

John Nash invented in 1949 a game called HEX, which is what we played on our first day of class. I like the Hex Wiki sight because they have downloadable boards which you can print at home so you can play HEX at home.  And if the students want to really refine their skills, they can play against the computer on the MazeWorks site.    To learn the game, we played some medium sized boards.

5x5 HEX Board

HEX consists of hexagons arranged in a rhombas.  Players take turns trying to make a path across the boards.  Once the students were familiar with the rules of the game, we analyzed heuristics and strategies for the game.  We spent some time discussing the 2x2 board. Under the guidance of Gilman, I named the two players Firstus and Secondus.  Firstus tries to go from one white side to the other.  Secondus tries to go from one black side to the other.   Many of the students assumed that Firstus would always win the 2x2 game.  But after further investigation, we realized the Secondus could win the game.  So I had four questions for the students (taken from Gilman)

1.  Can Firstus Win?  How or why not?

2. Can Secondus Win? How or why not?

3.  Can Firstus ensure a Win?  How or why not?

4.  Can Secondus ensure a Win? How or why not?

After playing the 3x3 version of the game, I asked the students to think about these questions for homework.  Can they develop a Winning strategy for the 3x3 game?  I am sure they can.

I also gave them some 4x4 boards, and 5x5 boards.  I asked them to try and devise a winning strategy for these games.  This is a bit challenging and would take some time.

What is a strategy?  A strategy would be the complete set of possible moves which will guarantee the win.  So this is much more complex than a heuristic, which would be for only one move.

So please have fun playing HEX with your children.  Not only is it a fun game, there is some interesting mathematics behind it.  In he coming few weeks I hope to study the Keypad Problem and the Game of Nim.
We had a reporter from the Daily Free Press visiting us today, so we might see some photos of the students in the local.

If you child gets really into HEX, there are versions of the game available. and instructions on the HEX Wiki site on how to build boards.

HEX Board Game

Parker Brothers HEX Game from early 1950s

Today, Pernille France, the head of LEGO Mindstorms from Denmark paid a visit to the CEEO.  It was really cool to listen about the news things happening.

Earlier in the month there was a STEM EXPO in Melrose.  I loaded up Bruce the Textrix Bird and a whole bunch of NXT bots into Dave McAndrews car for this fun event to make some candy pusher robots. Candy Pusher Robot

This past month I ran several LEGO workshops at the Roosevelt School and the Horace Mann school in Melrose for 5th grade students. There was a nice article in the newspaper today about the workshops.

The students used Robolab which was written at the Tufts CEEO. We used the Pilot version of Robolab.  If you want to learn about LEGO Robots, look at the LEGO Engineering web-site run by Tufts.

Laptops running Robolab Pilot

In the morning, the students learned to use Robolab to make LEGO RCX robots move back and forth.  LEGO RCX kits are discontinued, but you can buy them on Craig's List or E-bay.  If you want a new LEGO Robot kit, you can buy the LEGO NXT Kit.

LEGO RCX robot

Later in the morning, the robots were programmed to kick a ball, respond to a touch sensor, and do simple line tracking.

LEGO Robot with a ball kicker

Line tracking in the Green City

In the afternoon, the kids played a game from LEGO called the Green City Challenge.

Green City Challenge with Windmill

Tonight I served on a panel discussion along with Meredith (from the CEEO).  I wanted to mention several link from my presentation.  First, my presentation did not use Power Point, but used Prezi, which emphasizes connections between topics and the non-linear nature of discussions after a presentation.

I discussed the Science Team and mentioned several competitions where a science team could compete such as Science Olympiad, The Western Suburban Science League, the North Shore Science League, and the Science Bowl.  And I had to give a push for the Eastern Mass Physics Olympics which I am running.  I also had an interesting question as to what it takes to have a successful science team.  In short, interested students, a "team" of motivated teachers/mentors, and funding (for materials, transportation, uniforms, and stipends for those coaches).

I also discussed what goes into making a good research program.  I wanted to provide links for students who want to publish their work or their results: including the INTEL Science Search, Westinghouse Competition, the Junior Science and Humanities Symposium, the Davidson Institute, and the Journal of Experimental Secondary Science.  Some team based competition I like can be found at the NASA Teaching From Space website.  This is where I learned about the opportunity to have my students design an experiment which I got to fly on the vomit comet. You can read about a lot of NASA opportunities in my mid-October blog post.

I also gave a push for the Melrose Robotics team, the iRaiders.   You can see students from Roosevelt and Melrose Middles School compete at the Boston University Academy FIRST LEGO League competition on December 10th!  You can see students from Melrose Middle School compete at the BUA VEX Robotics Competition on January 16th.

The summer programs at BU I wanted to promote include U-Design (engineering for Middle School students where I teach aviation and rocket science), Pathways, PROMYS, and Citylab.

And as a push for the great LEGO programs at the Tufts CEEO, check out the workshops we host there!